Ratio Tables: Moving to Generalisation

Yesterday was MathsConf33, which was exciting for a number of reasons:

I love a maths conference and a chance to see all my pals and be geeky with them.
This time around, the conference was held 20 mins from my house, so I didn’t need to pay for a hotel!
I got to present under my new name and new title for the first time!

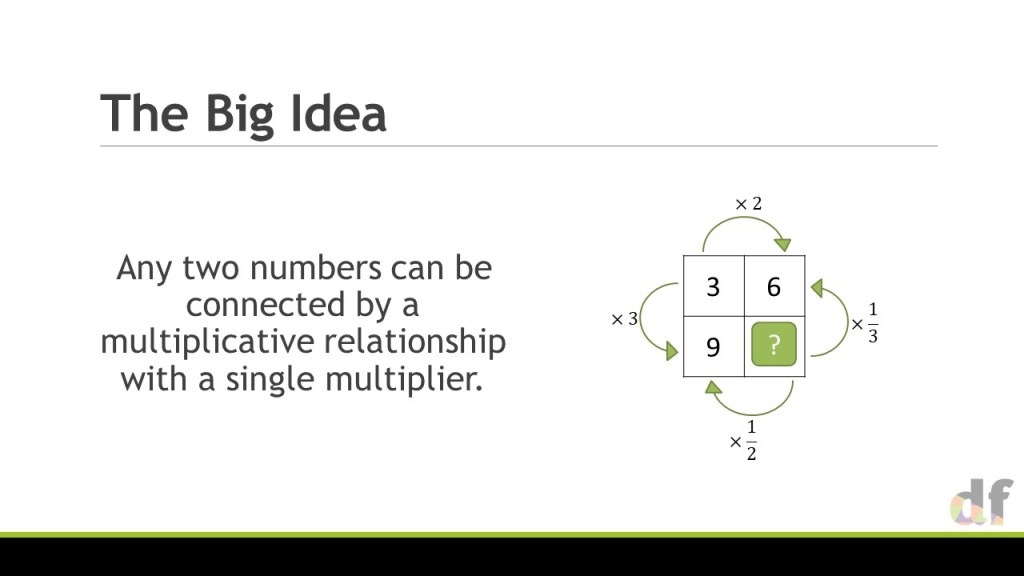
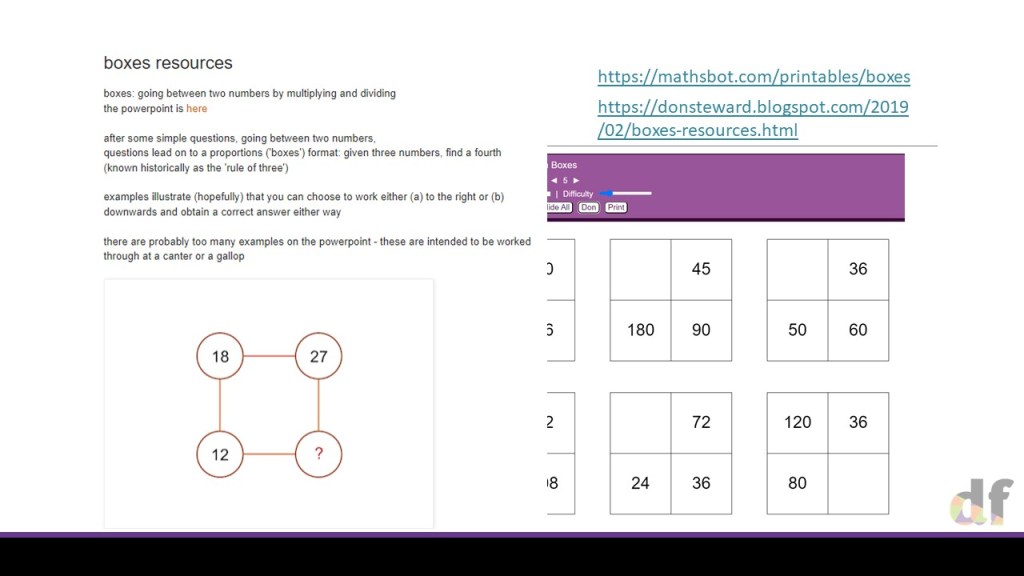
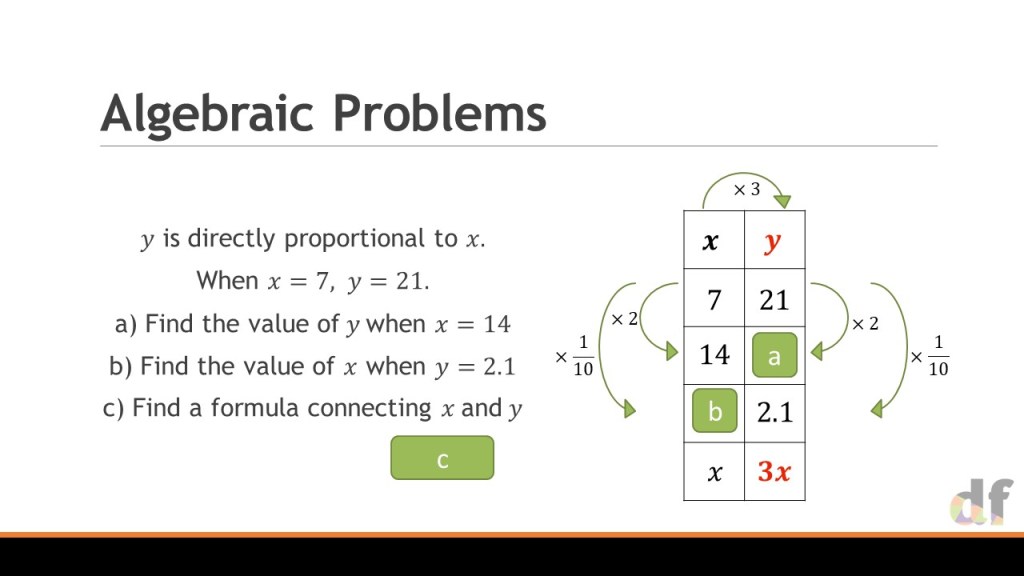
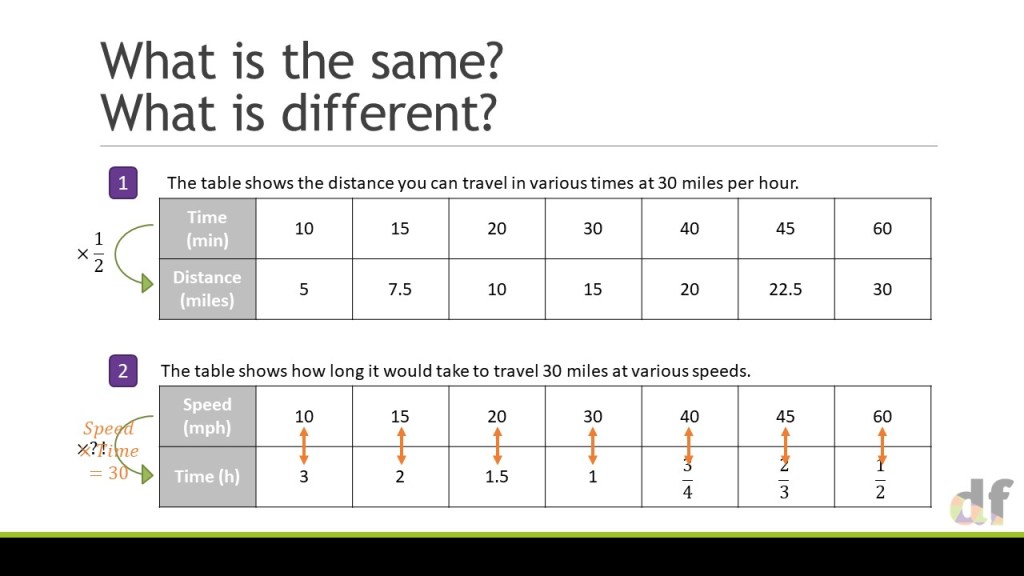
I have been raving about the utility of ratio tables for a couple of years now, and in my last MathsConf session I showed the versatility of them for topics across the curriculum. I ended with a snapshot of how I use them for algebraic direct proportion questions. People went a bit mad for it, and since then the biggest questions I have had have been about how to extend this idea, so I decided it was high time to share the specifics some more.

I’d like to take a moment to apologise for the countless typos and tripping over my words a little – I have recently had COVID, and it has really muddled my brain and made me much more tired than usual, so I feel I wasn’t up to my usual standard! The typos have been corrected, and there is some more commentary on the more complex questions and ideas below. You should also be able to download the (corrected) slides at the bottom of the post.

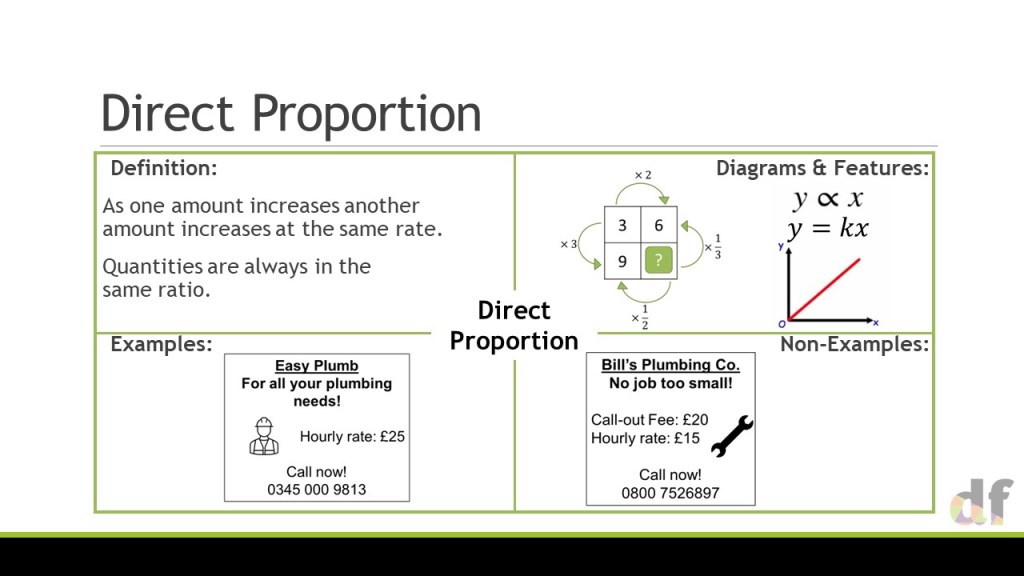
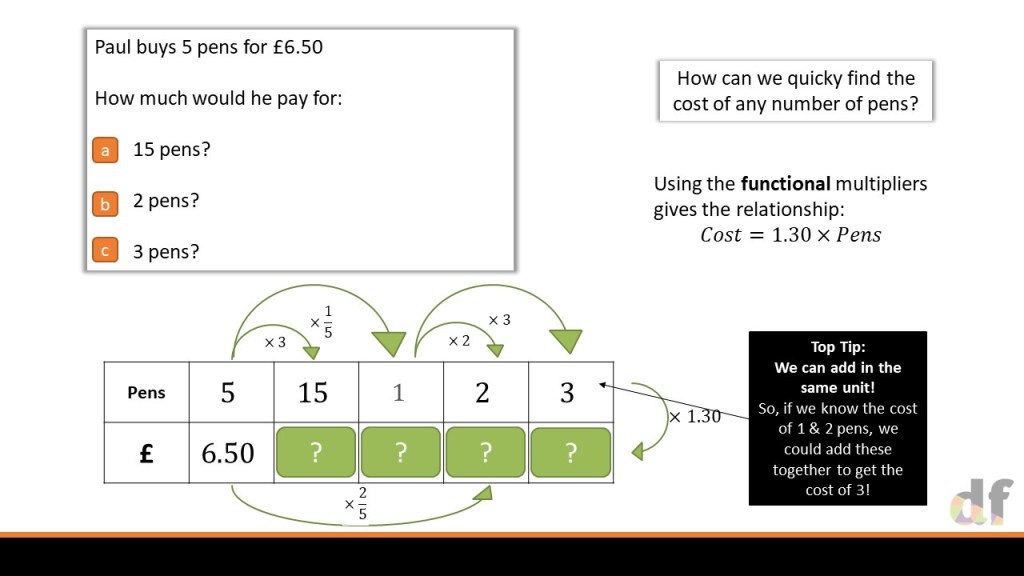
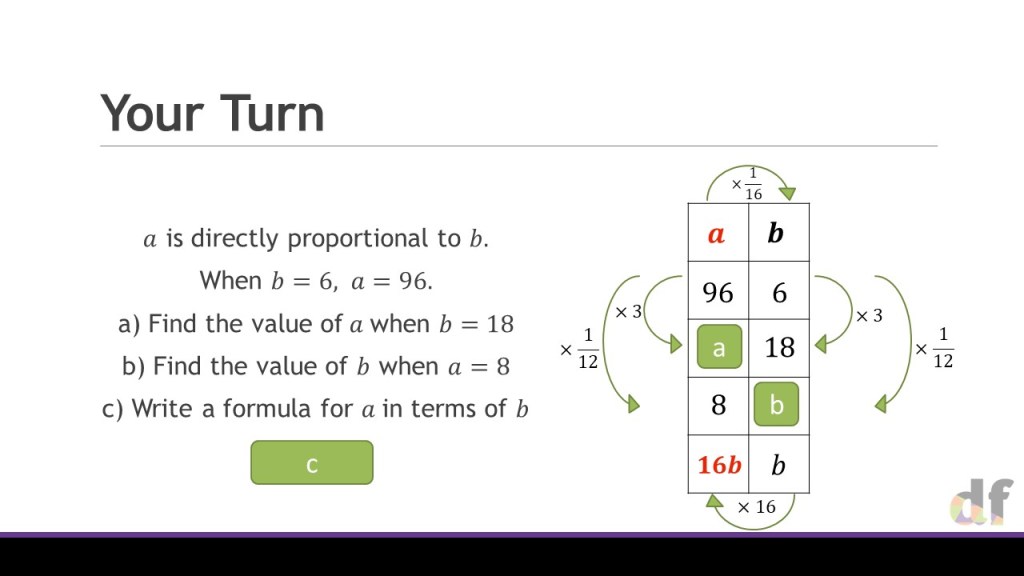
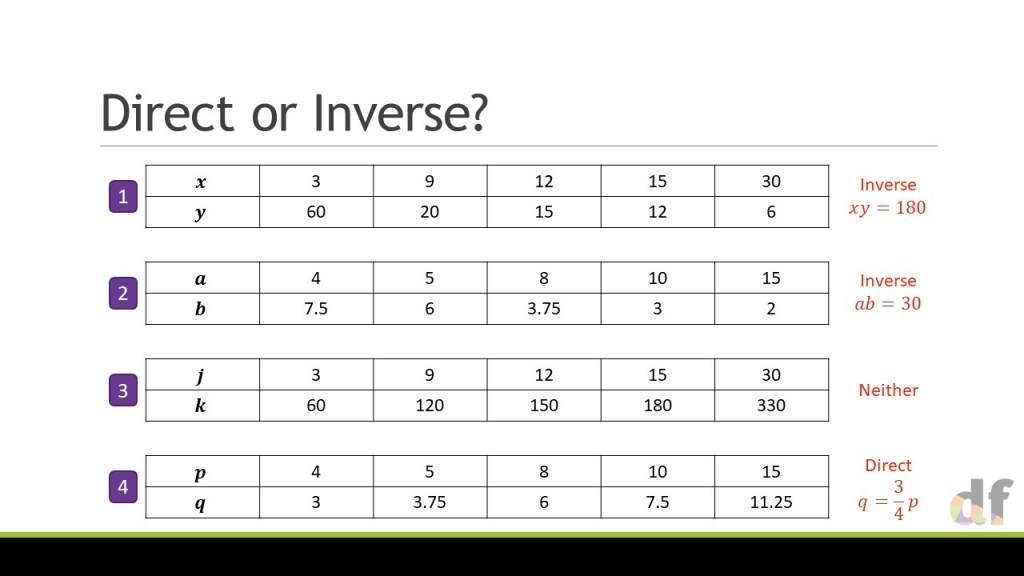
For me, this approach feels like a really natural extension to the ideas I had shared with numerical problems, but popping in variables to the table instead! However, there is always some complexity with algebraic proportion, in that these relationships don’t always have to be linear. So I decided to show you how I have approached this with my classes in the last 2 years, and what has worked well.

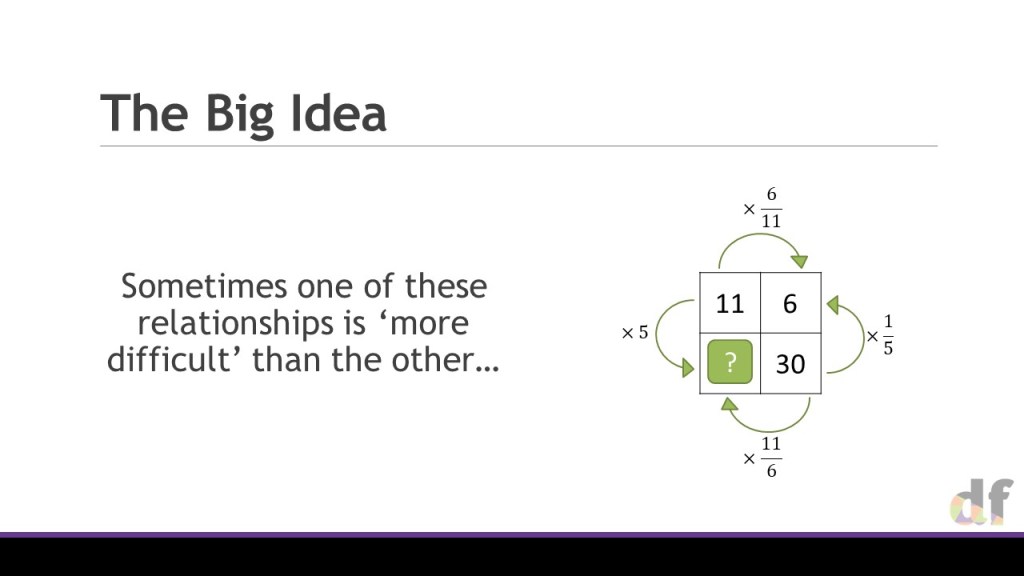
One the whole, this involves adding extra columns to the table, and being very very careful about where the proportionality lies. As such, I only use my ‘outside’ arrows to show this. Through the slides we gradually build in complexity with non-linear relationships and multiple variables. Through this, I cement a huge point that I believe we often miss in the teaching of proportionality; If a is proportional to b, and then b is proportional to c, then we don’t need to consider two multipliers – just one, that combines them both. The ratio table makes this really clear, and I am a big fan of it in this instance.

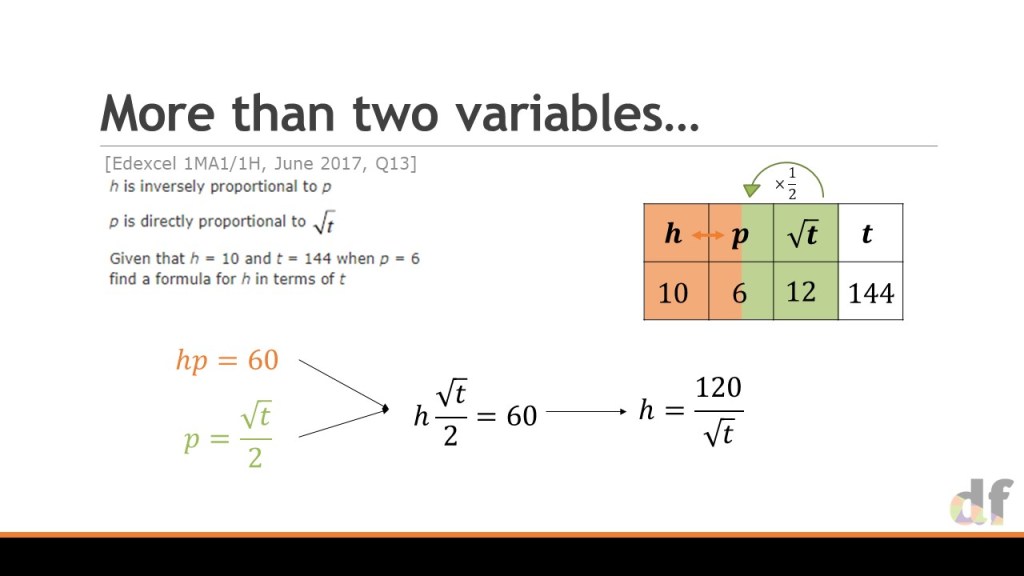
However, I then came across this exam question, and it has two sets of non-linear direct proportionality… This problem is on slide 25 (and in the image below), and I don’t feel I caveated properly yesterday. I did this problem in a ratio table more as a thought exercise for myself, as I haven’t seen many questions like it, and I kind of wanted to prove that it could be done. But I am not convinced that it would be the best way to do it in the classroom. In fact, I think at this stage, it is just as complex as working with substitution, as you are jumping around the table so much and effectively ending up with three statements of equality for one variable…

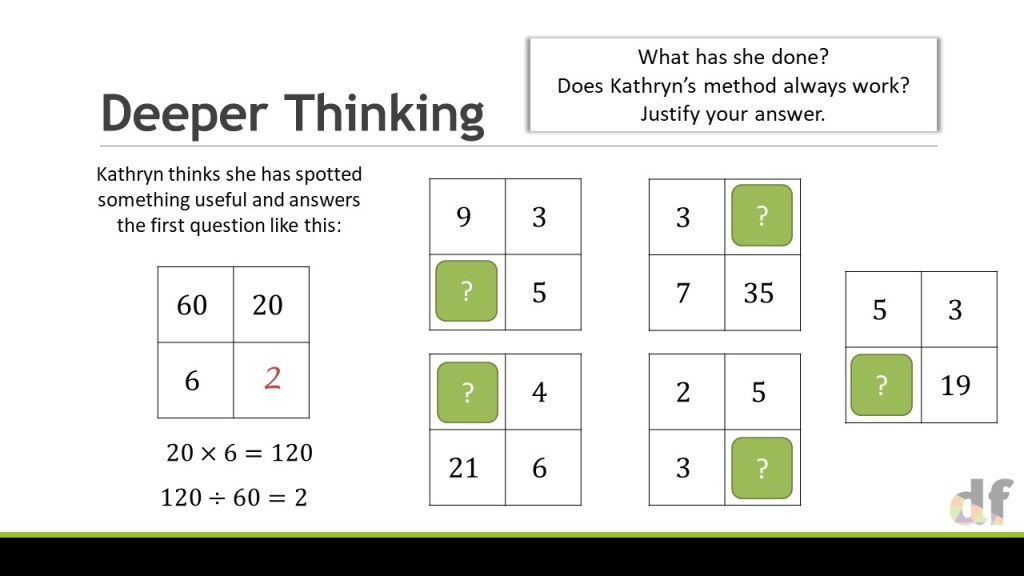
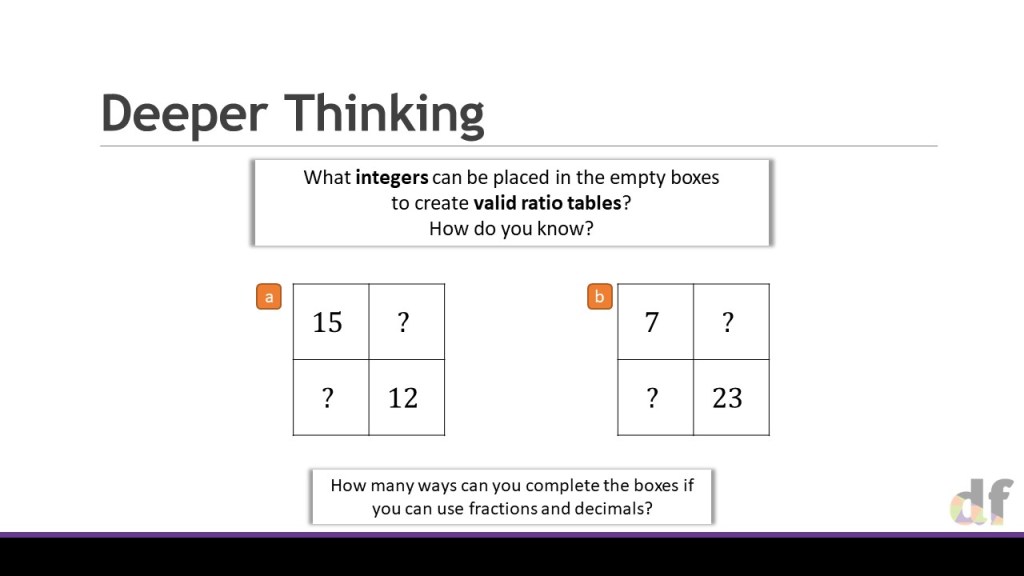
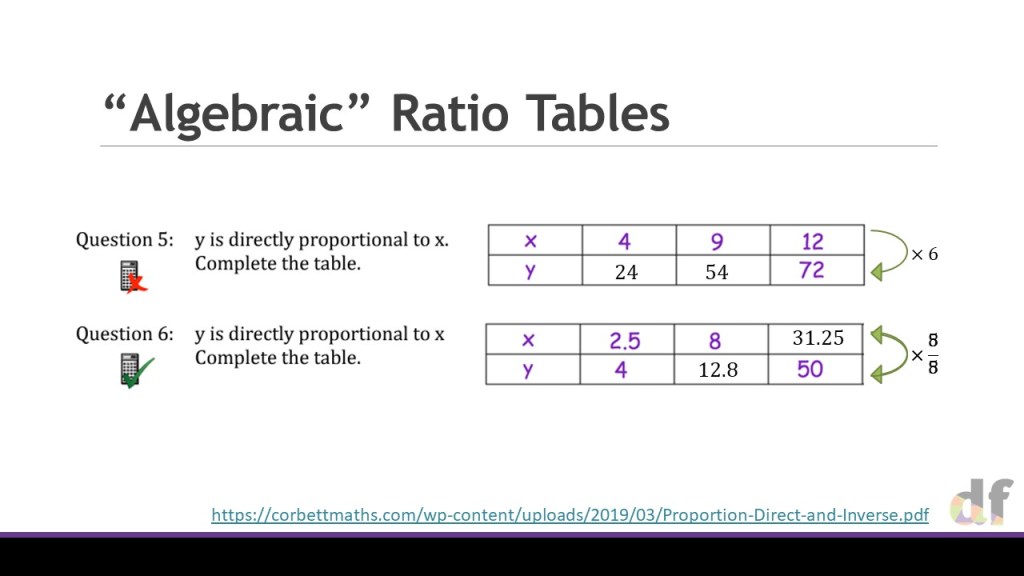
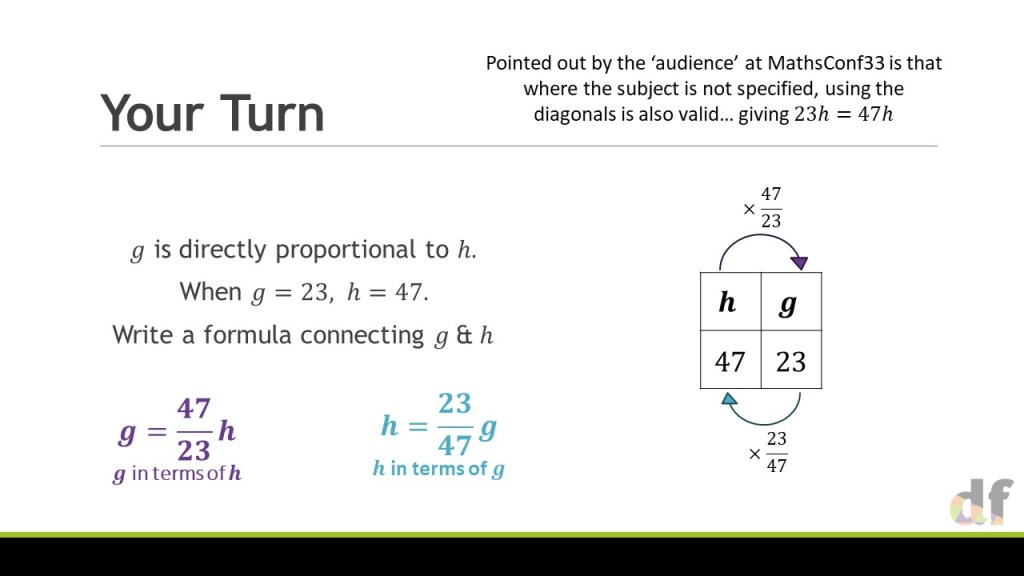
So, for the sake of clarity, at the stage of coming to problems like this, I am not advocating that the ratio table is the best or “easiest” way forward. What I am arguing is that using the same representation consistently is key to building the conceptual understanding that multiplicative relationships are structurally no different in a generalised algebraic form.

I would hope that by the time your students reach questions like the one above, that the tables have helped them to see that these relationships always boil down to y=kf(x) . The structure has been exposed by our consistency with use of the ratio table, and they can then move towards solving these much more sophisticated problems. At this stage, they can use whatever method feels best, ratio table or algebraic substitution, to help them get to the final formulae.

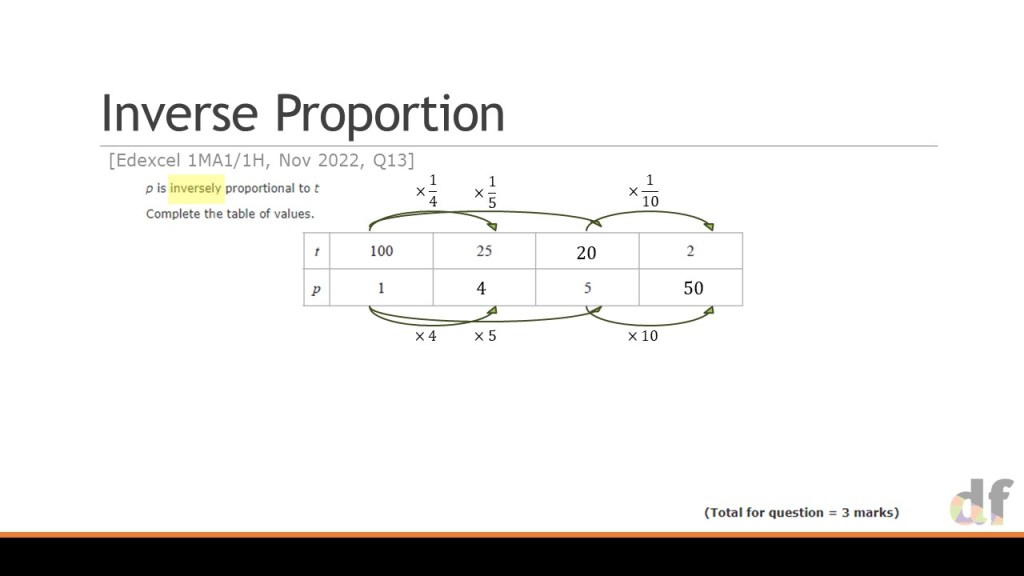
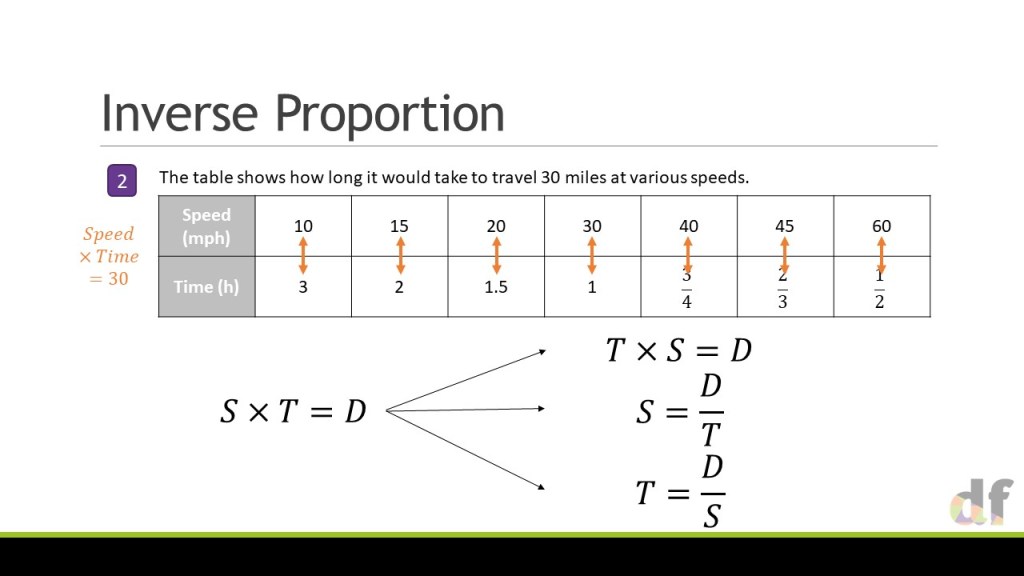
I began looking at inverse proportion towards the end of this session, but as usual had massively over planned! I think I got to slide 31 before we ran out of time! I have included the others in the download, so if you are curious then you can have a look through and let me know if you have any questions. If you think a session exclusively on inverse proportion would be useful at another conference, please let me know!

Other than that, all that is left is to say “thank you” so much for coming yesterday – it was nice to have so many people come to my session when I was billed against Mark McCourt! You all asked so many great questions and engaged with me as colleagues in a way that really matured my ideas, which is why I love MathsConfs so much. I am excited to spend some time thinking about it all and improving the approach for when I make the lessons on the topic for Dr Frost!

I’d also like to say thank you to everyone who shared their ideas through the day. I loved every session I went to and enjoyed thinking hard in a room full of fellow geeks. A particularly large shoutout to my fellow ratio and proportion lovers – we seemed to be out in force yesterday!